Erika McCarthy1, Şölen Ekesan1, and Darrin M. York1
1Laboratory for Biomolecular Simulation Research, Institute for Quantitative Biomedicine and Department of Chemistry and Chemical Biology, Rutgers University, Piscataway, NJ 08854, USA
In this tutorial you will learn how to apply a machine learning potential correction (ΔMLP) to semiempirical (DFTB3) simulations and validate the resulting free energy surface using generalized weighted thermodynamic perturbation (gwTP). The tutorial is structured as follows:
The necessary inputs for part 1.1 are available in:
/expanse/projects/qstore/amber_ws/tutorials/MLP-gwTP_MTR1/PBE0_timingtest/inputs
and
/expanse/projects/qstore/amber_ws/tutorials/MLP-gwTP_MTR1/MLP_timingtest/inputs
The subsequent outputs are available in:
/expanse/projects/qstore/amber_ws/tutorials/MLP-gwTP_MTR1/PBE0_timingtest/outputs
and
/expanse/projects/qstore/amber_ws/tutorials/MLP-gwTP_MTR1/MLP_timingtest/outputs
The inputs should be copied to your working directory. If you unable to produce an output for a given step, copy it from the output directory in order to proceed.
[user@cluster] mkdir PBE0_timingtest
[user@cluster] cp -r /expanse/projects/qstore/amber_ws/tutorials/MLP-gwTP_MTR1/PBE0_timingtest/inputs/* ./PBE0_timingtest
[user@cluster] mkdir MLP_timingtest
[user@cluster] cp -r /expanse/projects/qstore/amber_ws/tutorials/MLP-gwTP_MTR1/MLP_timingtest/inputs/* ./MLP_timingtestHere we will perform a short timing test to demonstrate the speed-up enabled by a ΔMLP compared to an ab initio level calculation. The ΔMLP was trained to correct DFTB3 level energies and forces to replicate PBE0/6-31G* for the MTR1 reaction. First we will run 2 steps of dynamics on a single umbrella window at the PBE0 level using the AMBER interface to QUICK. Simulations using QUICK can be accelerated using a GPU, but in order to stably use comparable electrostatic methods the test will be performed on a CPU. You have been provided img01_PBE0.mdin run_PBE0.slurm, img01.disang, init01.rst7, and a template directory containing the parm file.
PBE0
&cntrl
! IO =======================================
irest = 0 ! 0 = start, 1 = restart
ntx = 1 ! 1 = start, 5 = restart
ntxo = 1 ! read/write rst as formatted file
iwrap = 1 ! wrap crds to unit cell
ioutfm = 1 ! write mdcrd as netcdf
imin = 0
ntmin = 1
ntpr = 1
ntwr = 1
ntwx = 1
ntwf = 0
! DYNAMICS =================================
nstlim = 2 ! number of time steps
dt = 0.001 ! ps/step
ntb = 1 ! 1=NVT periodic, 2=NPT periodic, 0=no box
! TEMPERATURE ==============================
temp0 = 298 ! target temp
gamma_ln = 5.0 ! Langevin collision freq
ntt = 3 ! thermostat (3=Langevin)
! PRESSURE ================================
ntp = 0 ! 0=no scaling, 1=isotropic, 2=anisotropic
! SHAKE ====================================
ntc = 2 ! 1=no shake, 2=HX constrained, 3=all constrained
noshakemask = ":69|@272-282,290-291,1975-1988" ! do not shake these
ntf = 1 ! 1=cpt all bond E, 2=ignore HX bond E, 3=ignore all bond E
! MISC =====================================
cut = 10.0
ifqnt = 1
ig = -1
nmropt = 1
/
&wt
type='DUMPFREQ', istep1=1
&end
&wt
type='END',
&end
DISANG=img01.disang
DUMPAVE=img01.dumpave
&ewald
dsum_tol = 1.e-6
/
&qmmm
qm_theory = 'quick'
qmmask = ':69|@272-282,290-291,1975-1988'
qmcharge = 1
spin = 1
qmmm_int = 1
qm_ewald = 1
qmshake = 0
itrmax = 50
scfconv = 1e-07
verbosity = 0
/
&quick
method = 'PBE0'
basis = '6-31G*'
/
Note the inclusion of the quick namelist specifying the functional and basis set for the simulation.
[user@cluster] sbatch run_PBE0.slurm You will find that the job takes about 6 minutes to complete. While it runs, let's take a look at the input for the QM/MM+ΔMLP simulation. You have been provided img01_MLP.mdin and run_MLP.slurm. The template directory also contains 4 graph files that each contain a set of machine learning model parameters.
MLP
&cntrl
! IO =======================================
irest = 0 ! 0 = start, 1 = restart
ntx = 1 ! 1 = start, 5 = restart
ntxo = 1 ! read/write rst as formatted file
iwrap = 1 ! wrap crds to unit cell
ioutfm = 1 ! write mdcrd as netcdf
imin = 0
ntmin = 1
ntpr = 1
ntwr = 1
ntwx = 1
ntwf = 0
! DYNAMICS =================================
nstlim = 2 ! number of time steps
dt = 0.001 ! ps/step
ntb = 1 ! 1=NVT periodic, 2=NPT periodic, 0=no box
! TEMPERATURE ==============================
temp0 = 298 ! target temp
gamma_ln = 5.0 ! Langevin collision freq
ntt = 3 ! thermostat (3=Langevin)
! PRESSURE ================================
ntp = 0 ! 0=no scaling, 1=isotropic, 2=anisotropic
! SHAKE ====================================
ntc = 2 ! 1=no shake, 2=HX constrained, 3=all constrained
noshakemask = ":69|@272-282,290-291,1975-1988" ! do not shake these
ntf = 1 ! 1=cpt all bond E, 2=ignore HX bond E, 3=ignore all bond E
! MISC =====================================
cut = 10.0
ifqnt = 1
ig = -1
nmropt = 1
/
&ewald
dsum_tol = 1.e-6
/
&qmmm
qm_theory = 'DFTB3'
qmmask = ':69|@272-282,290-291,1975-1988'
qmcharge = 1
spin = 1
qmshake = 0
qm_ewald = 1
qmmm_switch = 1
scfconv = 1.e-10
verbosity = 0
tight_p_conv = 1
diag_routine = 0
pseudo_diag = 1
dftb_maxiter = 100
/
&wt type = 'DUMPFREQ', istep1 = 1, /
&wt type='END' /
DISANG=img01.disang
DUMPAVE=img01.dumpave
LISTOUT=POUT
LISTIN=POUT
&dprc
idprc=1
mask=":69|@272-282,290-291,1975-1988"
rcut = 6.0
intrafile=""
interfile(1)="template/graph.000.pb"
/
The dprc namelist indicates that we will be using the interface to DeePMD-Kit to apply a Deep Potential Range Correction model (ie the ΔMLP). Here we will also run 2 steps of dynamics.
[user@cluster] sbatch run_MLP.slurm When the jobs are complete, compare the mdinfo files.
NSTEP = 2 TIME(PS) = 0.002 TEMP(K) = 12.93 PRESS = 0.0
Etot = -1139551.3377 EKtot = 1488.8508 EPtot = -1141040.1886
BOND = 548.5419 ANGLE = 1093.1544 DIHED = 1635.9114
1-4 NB = 624.7780 1-4 EEL = -7539.0600 VDWAALS = 36590.5463
EELEC = -268485.1838 EHBOND = 0.0000 RESTRAINT = 2.6047
QUICKESCF= -905511.4815
EAMBER (non-restraint) = -1141042.7932
Ewald error estimate: 0.1108E-04
NMR restraints: Bond = 0.000 Angle = 0.000 Torsion = 0.000
: Gen. Dist. Coord. = 2.605
===============================================================================
| Final Performance Info:
| -----------------------------------------------------
| Average timings for last 1 steps:
| Elapsed(s) = 119.75 Per Step(ms) = 119753.32
| ns/day = 0.00 seconds/ns = **********
|
| Average timings for all steps:
| Elapsed(s) = 348.89 Per Step(ms) = 174444.74
| ns/day = 0.00 seconds/ns = **********
| ----------------------------------------------------- NSTEP = 2 TIME(PS) = 0.002 TEMP(K) = 12.96 PRESS = 0.0
Etot = -1139551.1318 EKtot = 1492.0009 EPtot = -1141043.1327
BOND = 548.9066 ANGLE = 1092.8042 DIHED = 1635.5829
1-4 NB = 624.7320 1-4 EEL = -7539.0003 VDWAALS = 36587.1481
EELEC = -268484.2609 EHBOND = 0.0000 RESTRAINT = 2.5503
DFTBESCF= -5216.9778
ML = -900294.6180
EAMBER (non-restraint) = -1141045.6830
Ewald error estimate: 0.1211E-01
NMR restraints: Bond = 0.000 Angle = 0.000 Torsion = 0.000
: Gen. Dist. Coord. = 2.550
===============================================================================
| Final Performance Info:
| -----------------------------------------------------
| Average timings for last 1 steps:
| Elapsed(s) = 0.54 Per Step(ms) = 540.10
| ns/day = 0.16 seconds/ns = 540099.98
|
| Average timings for all steps:
| Elapsed(s) = 13.63 Per Step(ms) = 6812.91
| ns/day = 0.01 seconds/ns = 6812913.00
| -----------------------------------------------------In general, the first step of dynamics is always the slowest, so for an accurate comparison, one should look at the timing for the last step. This took 119.75 seconds per step with PBE0 and 0.54 seconds per step with the ΔMLP. The ΔMLP provides a significant speed-up over the ab initio simulation, and as you will demonstrate in the next section, it does so with high accuracy.
Section 1.2 will walk you through a set of simulations that have already been performed. The necessary inputs for those simulations are available in:
/expanse/projects/qstore/amber_ws/tutorials/MLP-gwTP_MTR1/gwTP/input
The subsequent outputs for you to analyze are available in:
/expanse/projects/qstore/amber_ws/tutorials/MLP-gwTP_MTR1/gwTP/output
[user@cluster] mkdir MLP-gwTP
[user@cluster] cd MLP-gwTP
[user@cluster] cp -r /expanse/projects/qstore/amber_ws/tutorials/MLP-gwTP_MTR1/gwTP/output ./
[user@cluster] cd outputNext you will learn how to validate the accuracy of the ΔMLP model using gwTP, but first we will review how the data was generated. These simulations and calculations would take longer than there is time for in this exercise, thus the results have been provided for you. You have been given data in which 3 iterations of the SASM (it08, it09, it10) was performed near the final path, each for 4 trials (000, 001, 002, 003). The 4 trials each apply 1 of the 4 graph files in the template directory when running the simulations. These 4 sets of neural network parameters were generated stochastically when the training was performed using the DeePMD-Kit program. They serve as multiple reference Hamiltonians for gwTP. If one model is deficient in a particular area of the free energy surface, another model will likely perform better, and will thus be favored during reweighting.
As an example, let's focus on the directory it08_000.
[user@cluster] ls it08_000
img01.disang img04.mdin img07.rst7 img11.dumpave img14.mdout img18.disang img21.mdin img24.rst7 img28.dumpave img31.mdout
img01.dumpave img04.mdout img08.disang img11.mdin img14.rst7 img18.dumpave img21.mdout img25.disang img28.mdin img31.rst7
img01.mdin img04.rst7 img08.dumpave img11.mdout img15.disang img18.mdin img21.rst7 img25.dumpave img28.mdout img32.disang
img01.mdout img05.disang img08.mdin img11.rst7 img15.dumpave img18.mdout img22.disang img25.mdin img28.rst7 img32.dumpave
img01.rst7 img05.dumpave img08.mdout img12.disang img15.mdin img18.rst7 img22.dumpave img25.mdout img29.disang img32.mdin
img02.disang img05.mdin img08.rst7 img12.dumpave img15.mdout img19.disang img22.mdin img25.rst7 img29.dumpave img32.mdout
img02.dumpave img05.mdout img09.disang img12.mdin img15.rst7 img19.dumpave img22.mdout img26.disang img29.mdin img32.rst7
img02.mdin img05.rst7 img09.dumpave img12.mdout img16.disang img19.mdin img22.rst7 img26.dumpave img29.mdout path.micro.pkl
img02.mdout img06.disang img09.mdin img12.rst7 img16.dumpave img19.mdout img23.disang img26.mdin img29.rst7 path.sims.pkl
img02.rst7 img06.dumpave img09.mdout img13.disang img16.mdin img19.rst7 img23.dumpave img26.mdout img30.disang pathconv.txt
img03.disang img06.mdin img09.rst7 img13.dumpave img16.mdout img20.disang img23.mdin img26.rst7 img30.dumpave reanalysis
img03.dumpave img06.mdout img10.disang img13.mdin img16.rst7 img20.dumpave img23.mdout img27.disang img30.mdin rem.08.log
img03.mdin img06.rst7 img10.dumpave img13.mdout img17.disang img20.mdin img23.rst7 img27.dumpave img30.mdout rem.type
img03.mdout img07.disang img10.mdin img13.rst7 img17.dumpave img20.mdout img24.disang img27.mdin img30.rst7 samplingconv.txt
img03.rst7 img07.dumpave img10.mdout img14.disang img17.mdin img20.rst7 img24.dumpave img27.mdout img31.disang sims.txt
img04.disang img07.mdin img10.rst7 img14.dumpave img17.mdout img21.disang img24.mdin img27.rst7 img31.dumpave
img04.dumpave img07.mdout img11.disang img14.mdin img17.rst7 img21.dumpave img24.mdout img28.disang img31.mdin You have previously learned how to perform string simulations. When running the string, one must output the trajectory if gwTP is to be performed. Trajectories are omitted here for the sake of file size, but the reaction coordinates for analysis are captured in the dumpave files. For each trajectory generated by the string simulation, the structure was reanalyzed using a series of single point calculations with each ΔMLP model and PBE0. Reanalysis can be performed using SANDER by setting imin = 6 and nmropt = 0 in the mdin file.
snglpt
&cntrl
! IO =======================================
irest = 0 ! 0 = start, 1 = restart
ntx = 1 ! 1 = start, 5 = restart
ntxo = 1 ! read/write rst as formatted file
iwrap = 1 ! wrap crds to unit cell
ioutfm = 1 ! write mdcrd as netcdf
imin = 6 ! Perform single points on structures in an nc file
ntmin = 1
ntpr = 1
ntwr = 0
ntwx = 0
ntwf = 0
ntwe = 0
! DYNAMICS =================================
nstlim = 0 ! number of time steps
dt = 0.001 ! ps/step
ntb = 1 ! 1=NVT periodic, 2=NPT periodic, 0=no box
! TEMPERATURE ==============================
temp0 = 298 ! target temp
gamma_ln = 5.0 ! Langevin collision freq
ntt = 3 ! thermostat (3=Langevin)
! PRESSURE ================================
ntp = 0 ! 0=no scaling, 1=isotropic, 2=anisotropic
! SHAKE ====================================
ntc = 2 ! 1=no shake, 2=HX constrained, 3=all constrained
noshakemask = ":69|@272-282,290-291,1975-1988" ! do not shake these
ntf = 1 ! 1=cpt all bond E, 2=ignore HX bond E, 3=ignore all bond E
! MISC =====================================
cut = 10.0
ifqnt = 1
ig = -1
nmropt = 0
/
&ewald
dsum_tol = 1.e-6
/
&qmmm
qm_theory = 'DFTB3'
qmmask = ':69|@272-282,290-291,1975-1988'
qmcharge = 1
spin = 1
qmshake = 0
qm_ewald = 1
qmmm_switch = 1
scfconv = 1.e-10
verbosity = 0
tight_p_conv = 1
diag_routine = 0
pseudo_diag = 1
dftb_maxiter = 100
/
&wt type = 'DUMPFREQ', istep1 = 8, /
&wt type='END' /
DISANG=img01.disang
DUMPAVE=img01.dumpave
LISTOUT=POUT
LISTIN=POUT
/
&dprc
idprc=1
mask=":69|@272-282,290-291,1975-1988"
rcut = 6.0
intrafile=""
interfile(1)="../../template/graph.000.pb"
/The output of the single point calculations are in the reanalysis directory. These will be used as input for gwTP in the next section.
[user@cluster] cd it08_000/reanalysis
[user@cluster] ls *mdout
ene_img01_DFTB3_ML000.mdout ene_img09_DFTB3_ML000.mdout ene_img17_DFTB3_ML000.mdout ene_img25_DFTB3_ML000.mdout
ene_img01_DFTB3_ML001.mdout ene_img09_DFTB3_ML001.mdout ene_img17_DFTB3_ML001.mdout ene_img25_DFTB3_ML001.mdout
ene_img01_DFTB3_ML002.mdout ene_img09_DFTB3_ML002.mdout ene_img17_DFTB3_ML002.mdout ene_img25_DFTB3_ML002.mdout
ene_img01_DFTB3_ML003.mdout ene_img09_DFTB3_ML003.mdout ene_img17_DFTB3_ML003.mdout ene_img25_DFTB3_ML003.mdout
ene_img01_PBE0.mdout ene_img09_PBE0.mdout ene_img17_PBE0.mdout ene_img25_PBE0.mdout
ene_img02_DFTB3_ML000.mdout ene_img10_DFTB3_ML000.mdout ene_img18_DFTB3_ML000.mdout ene_img26_DFTB3_ML000.mdout
ene_img02_DFTB3_ML001.mdout ene_img10_DFTB3_ML001.mdout ene_img18_DFTB3_ML001.mdout ene_img26_DFTB3_ML001.mdout
ene_img02_DFTB3_ML002.mdout ene_img10_DFTB3_ML002.mdout ene_img18_DFTB3_ML002.mdout ene_img26_DFTB3_ML002.mdout
ene_img02_DFTB3_ML003.mdout ene_img10_DFTB3_ML003.mdout ene_img18_DFTB3_ML003.mdout ene_img26_DFTB3_ML003.mdout
ene_img02_PBE0.mdout ene_img10_PBE0.mdout ene_img18_PBE0.mdout ene_img26_PBE0.mdout
ene_img03_DFTB3_ML000.mdout ene_img11_DFTB3_ML000.mdout ene_img19_DFTB3_ML000.mdout ene_img27_DFTB3_ML000.mdout
ene_img03_DFTB3_ML001.mdout ene_img11_DFTB3_ML001.mdout ene_img19_DFTB3_ML001.mdout ene_img27_DFTB3_ML001.mdout
ene_img03_DFTB3_ML002.mdout ene_img11_DFTB3_ML002.mdout ene_img19_DFTB3_ML002.mdout ene_img27_DFTB3_ML002.mdout
ene_img03_DFTB3_ML003.mdout ene_img11_DFTB3_ML003.mdout ene_img19_DFTB3_ML003.mdout ene_img27_DFTB3_ML003.mdout
ene_img03_PBE0.mdout ene_img11_PBE0.mdout ene_img19_PBE0.mdout ene_img27_PBE0.mdout
ene_img04_DFTB3_ML000.mdout ene_img12_DFTB3_ML000.mdout ene_img20_DFTB3_ML000.mdout ene_img28_DFTB3_ML000.mdout
ene_img04_DFTB3_ML001.mdout ene_img12_DFTB3_ML001.mdout ene_img20_DFTB3_ML001.mdout ene_img28_DFTB3_ML001.mdout
ene_img04_DFTB3_ML002.mdout ene_img12_DFTB3_ML002.mdout ene_img20_DFTB3_ML002.mdout ene_img28_DFTB3_ML002.mdout
ene_img04_DFTB3_ML003.mdout ene_img12_DFTB3_ML003.mdout ene_img20_DFTB3_ML003.mdout ene_img28_DFTB3_ML003.mdout
ene_img04_PBE0.mdout ene_img12_PBE0.mdout ene_img20_PBE0.mdout ene_img28_PBE0.mdout
ene_img05_DFTB3_ML000.mdout ene_img13_DFTB3_ML000.mdout ene_img21_DFTB3_ML000.mdout ene_img29_DFTB3_ML000.mdout
ene_img05_DFTB3_ML001.mdout ene_img13_DFTB3_ML001.mdout ene_img21_DFTB3_ML001.mdout ene_img29_DFTB3_ML001.mdout
ene_img05_DFTB3_ML002.mdout ene_img13_DFTB3_ML002.mdout ene_img21_DFTB3_ML002.mdout ene_img29_DFTB3_ML002.mdout
ene_img05_DFTB3_ML003.mdout ene_img13_DFTB3_ML003.mdout ene_img21_DFTB3_ML003.mdout ene_img29_DFTB3_ML003.mdout
ene_img05_PBE0.mdout ene_img13_PBE0.mdout ene_img21_PBE0.mdout ene_img29_PBE0.mdout
ene_img06_DFTB3_ML000.mdout ene_img14_DFTB3_ML000.mdout ene_img22_DFTB3_ML000.mdout ene_img30_DFTB3_ML000.mdout
ene_img06_DFTB3_ML001.mdout ene_img14_DFTB3_ML001.mdout ene_img22_DFTB3_ML001.mdout ene_img30_DFTB3_ML001.mdout
ene_img06_DFTB3_ML002.mdout ene_img14_DFTB3_ML002.mdout ene_img22_DFTB3_ML002.mdout ene_img30_DFTB3_ML002.mdout
ene_img06_DFTB3_ML003.mdout ene_img14_DFTB3_ML003.mdout ene_img22_DFTB3_ML003.mdout ene_img30_DFTB3_ML003.mdout
ene_img06_PBE0.mdout ene_img14_PBE0.mdout ene_img22_PBE0.mdout ene_img30_PBE0.mdout
ene_img07_DFTB3_ML000.mdout ene_img15_DFTB3_ML000.mdout ene_img23_DFTB3_ML000.mdout ene_img31_DFTB3_ML000.mdout
ene_img07_DFTB3_ML001.mdout ene_img15_DFTB3_ML001.mdout ene_img23_DFTB3_ML001.mdout ene_img31_DFTB3_ML001.mdout
ene_img07_DFTB3_ML002.mdout ene_img15_DFTB3_ML002.mdout ene_img23_DFTB3_ML002.mdout ene_img31_DFTB3_ML002.mdout
ene_img07_DFTB3_ML003.mdout ene_img15_DFTB3_ML003.mdout ene_img23_DFTB3_ML003.mdout ene_img31_DFTB3_ML003.mdout
ene_img07_PBE0.mdout ene_img15_PBE0.mdout ene_img23_PBE0.mdout ene_img31_PBE0.mdout
ene_img08_DFTB3_ML000.mdout ene_img16_DFTB3_ML000.mdout ene_img24_DFTB3_ML000.mdout ene_img32_DFTB3_ML000.mdout
ene_img08_DFTB3_ML001.mdout ene_img16_DFTB3_ML001.mdout ene_img24_DFTB3_ML001.mdout ene_img32_DFTB3_ML001.mdout
ene_img08_DFTB3_ML002.mdout ene_img16_DFTB3_ML002.mdout ene_img24_DFTB3_ML002.mdout ene_img32_DFTB3_ML002.mdout
ene_img08_DFTB3_ML003.mdout ene_img16_DFTB3_ML003.mdout ene_img24_DFTB3_ML003.mdout ene_img32_DFTB3_ML003.mdout
ene_img08_PBE0.mdout ene_img16_PBE0.mdout ene_img24_PBE0.mdout ene_img32_PBE0.mdout Now that you know how the data was generated, you will learn how to perform gwTP to estimate the PBE0 level PMF from the sampling performed with the ΔMLP's.
Section 1.3 will continue in your working directory. If you have issue performing the analysis and wish to see the desired output, it can be found in gwTP-out which would have been copied from /expanse/projects/qstore/amber_ws/tutorials/MLP-gwTP_MTR1/gwTP/output.
You will need to use xmgrace to plot your results. This module conflicts with AMBER on Expanse, so it is recommended to open another Expanse window (be sure to use ssh -Y to enable the gui) and type:
module load cpu/0.15.4 intel/19.1.1.217 grace/5.1.25
to do the plotting tasks and avoid loading and unloading modules.
You have been provided a slurm script called run_gwTP.slurm and the file metafile.current in the gwTP directory.
#!/bin/bash
#SBATCH --job-name="rungwTP"
#SBATCH --output="gwTP.slurmout"
#SBATCH --error="gwTP.slurmerr"
#SBATCH --partition=shared
#SBATCH --nodes=1
#SBATCH --ntasks=1
#SBATCH --mem=4G
#SBATCH --cpus-per-task=8
#SBATCH --requeue
#SBATCH --export=ALL
#SBATCH -t 0:30:00
#SBATCH --account=gue998
#SBATCH --reservation=amber24
set -u
top=`pwd`
module load workshop/fetoolkit/default
export OMP_NUM_THREADS=8
export OPENBLAS_NUM_THREADS=8
disang=TEMPLATE.disang
cd ../
for it in {08..10}; do
for m in 0 1 2 3; do
echo "it${it}_00${m}"
cd it${it}_00${m}/reanalysis
if [ -d dumpaves_unbias ]; then
rm -r dumpaves_unbias
fi
if [ -f ML_HL_unbias.metafile ]; then
rm ML_HL_unbias.metafile
fi
mkdir dumpaves_unbias
if [[ "${m}" == "1" ]]; then
ham=1
elif [[ "${m}" == "2" ]]; then
ham=2
elif [[ "${m}" == "3" ]]; then
ham=3
else
ham=0
fi
for R in $(seq -w 1 1 32); do
BASE=img${R}
PBE0=img${R}_PBE0
ML0=${BASE}_DFTB3_ML000
ML1=${BASE}_DFTB3_ML001
ML2=${BASE}_DFTB3_ML002
ML3=${BASE}_DFTB3_ML003
if [[ $(grep -r "5. TIMINGS" ene_${ML0}.mdout) ]] && [[ $(grep -r "5. TIMINGS" ene_${ML1}.mdout) ]] && [[ $(grep -r "5. TIMINGS" ene_${ML2}.mdout) ]] && \
[[ $(grep -r "5. TIMINGS" ene_${ML3}.mdout) ]] && [[ $(grep -r "5. TIMINGS" ene_${PBE0}.mdout) ]]; then
ndfes-PrepareAmberData.py -d ${BASE}.disang --hamidx ${ham} -i ${BASE}.dumpave -o dumpaves_unbias/${BASE}.dumpave -r 1 2 -b 3 4 5 6 7 8 --ene ene_${ML0}.mdout \
--ene ene_${ML1}.mdout --ene ene_${ML2}.mdout --ene ene_${ML3}.mdout --ene ene_${PBE0}.mdout >> ML_HL_unbias.metafile
else
echo "${BASE} did not finish. Check the output."
fi
done
cd ../../
done
done
cd ${top}
ndfes-CombineMetafiles.py --out all.unbias.metafile ../it08_00{0..3}/reanalysis/ML_HL_unbias.metafile ../it09_00{0..3}/reanalysis/ML_HL_unbias.metafile ../it10_00{0..3}/reanalysis/ML_HL_unbias.metafile
ndfes_omp --mbar --nham=10 -w 0.15 --nboot 50 -c all.unbias.metafile.chk all.unbias.metafile
for i in 9 5; do
ndfes-path_omp --ipath metafile.current --chk all.unbias.metafile.chk --npathpts 100 --nsplpts 400 --model ${i} --opath path.${i}.opt.dat --maxit 300 --akima --wavg=4 --wavg-niter=1
done
ndfes-path_omp --ipath metafile.current --chk all.unbias.metafile.chk --npathpts 32 --model 9 --opath path.9.RE.dat --akima --wavg=4 --wavg-niter=1The nested loop will run ndfes-PrepareAmberData.py for each window in each trial. The flags for this command are different from what we used previously when simply analyzing string data. Here, the --hamidx flag is used to specify which Hamiltonian was used to generate the simulation. The default is zero. Each --ene instance points to the mdout files that were produced during reanalysis. Here we have a total of 5 Hamiltonians (4 ΔMLP models and PBE0). Additionally we will remove the impact of the additional harmonic biasing potentials contained in the disang file. A metafile called ML_HL_unbias.metafile will be written to each reanalysis directory.
Next, the metafiles are combined from all of the iterations and trials to create all.unbias.metafile. The chk file all.unbias.metafile.chk is created from this metafile. In this chk file there are 10 Hamiltonians (models when referring to ndfes flags). These are the 4 ΔMLP models and PBE0, both with and without the additional biasing potentials removed. The first 5 sets are biased, and the second 5 are unbiased. We will focus on the later. Since the model indexes are 0 based, model 5 corresponds to the ΔMLP from graph file 000, and model 9 corresponds to the gwTP corrected free energy at the PBE0 level. We will analyze the free energy profiles from these models for comparison.
The ndfes-path_omp command is used to optimize the machine learning and PBE0 level paths on the respective free energy surfaces. Finally, the command is run again for model 9 (PBE0) to obtain reweighting entropies.
[user@cluster] sbatch run_gwTP.slurm [user@cluster] ls gwTP
all.unbias.metafile metafile.current path.5.opt.dat path.9.RE.dat.wavg.9.dat path.9.dat.xml run_gwTP.sh
all.unbias.metafile.chk path.5.dat path.5.opt.dat.wavg.5.dat path.9.RE.dat.xml path.9.opt.dat run_gwTP.slurm
gwTP.slurmerr path.5.dat.wavg.5.dat path.5.opt.dat.xml path.9.dat path.9.opt.dat.wavg.9.dat
gwTP.slurmout path.5.dat.xml path.9.RE.dat path.9.dat.wavg.9.dat path.9.opt.dat.xml
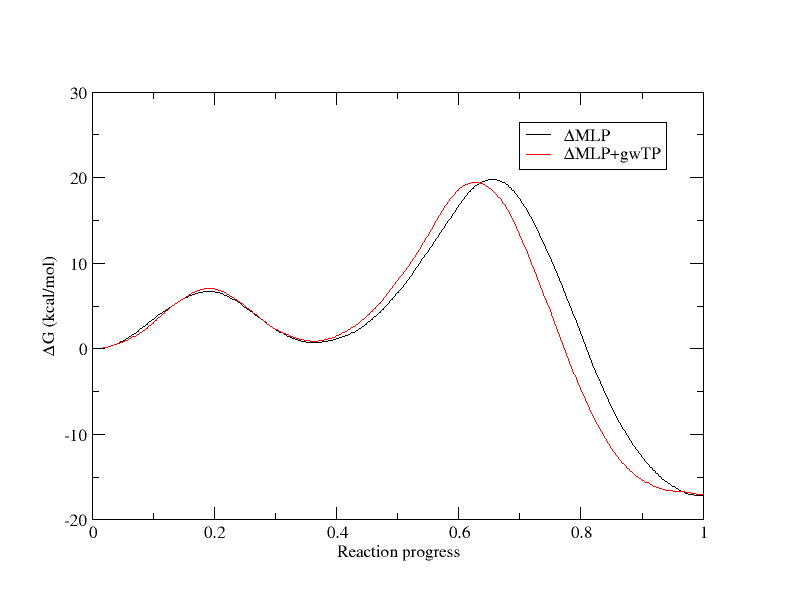
[user@cluster] xmgrace -block path.5.opt.dat.wavg.5.dat -bxy 2:5 -block path.9.opt.dat.wavg.9.dat -bxy 2:5 In the below plot the profiles have been aligned at y=0 for direct comparison.

The profiles are quite similar, with the machine learning potential yielding a rate determining barrier of 19.78 kcal/mol, and gwTP yielding a barrier of 19.43 kcal/mol, but there is still some discrepancy. How well did the machine learning potential do to correct DFTB3 to replicate PBE0? When gwTP is performed, the ndfes program computes an important metric called the reweighting entropy (RE). This is a number between 0 and 1 that effectively quantifies the phase space overlap between the reference and target potential in the bin containing a given point.
1 0.00000000000000e+00 -8.63471000000000e-01 -1.70990200000000e+00 1.790454e+01 0.095 0.829 145
2 3.22580645161290e-02 -7.23643099393740e-01 -1.64755575292408e+00 1.826003e+01 0.092 0.847 300
3 6.45161290322581e-02 -5.74876111556158e-01 -1.61191468070361e+00 1.921170e+01 0.097 0.648 321
4 9.67741935483871e-02 -4.21798346974683e-01 -1.60630825824268e+00 2.088689e+01 0.122 0.842 556
5 1.29032258064516e-01 -2.68708585473426e-01 -1.61432636055140e+00 2.278483e+01 0.099 0.791 383
6 1.61290322580645e-01 -1.15924404582858e-01 -1.62700192661683e+00 2.434311e+01 0.071 0.846 306
7 1.93548387096774e-01 3.67214780017976e-02 -1.64125858889227e+00 2.496843e+01 0.083 0.842 322
8 2.25806451612903e-01 1.89328263466230e-01 -1.65592773471958e+00 2.414705e+01 0.077 0.838 256
9 2.58064516129032e-01 3.42146139061666e-01 -1.66816784509145e+00 2.256895e+01 0.071 0.801 389
10 2.90322580645161e-01 4.95381667938472e-01 -1.67114524485306e+00 2.095009e+01 0.087 0.699 210
11 3.22580645161290e-01 6.45897165007477e-01 -1.64514630902587e+00 1.966024e+01 0.077 0.740 200
12 3.54838709677419e-01 7.70670034331531e-01 -1.55989348185740e+00 1.892839e+01 0.072 0.825 459
13 3.87096774193548e-01 8.37355743310727e-01 -1.42362410262515e+00 1.887799e+01 0.070 0.825 414
14 4.19354838709677e-01 8.58090289608902e-01 -1.27193527731017e+00 1.969304e+01 0.089 0.699 377
15 4.51612903225806e-01 8.61387996286766e-01 -1.11866117045908e+00 2.119472e+01 0.068 0.756 553
16 4.83870967741935e-01 8.63466229459934e-01 -9.65365197452351e-01 2.335955e+01 0.072 0.726 253
17 5.16129032258065e-01 8.66744262006695e-01 -8.12090178204530e-01 2.628068e+01 0.088 0.621 408
18 5.48387096774194e-01 8.68883904826271e-01 -6.58798066066249e-01 2.956726e+01 0.103 0.592 431
19 5.80645161290323e-01 8.68203679481171e-01 -5.05489469117158e-01 3.345300e+01 0.125 0.511 344
20 6.12903225806452e-01 8.67317707049999e-01 -3.52181808827297e-01 3.648824e+01 0.070 0.828 385
21 6.45161290322581e-01 8.66416734393529e-01 -1.98874235948492e-01 3.731200e+01 0.079 0.824 343
22 6.77419354838710e-01 8.65659808921910e-01 -4.55658939520789e-02 3.582405e+01 0.084 0.737 388
23 7.09677419354839e-01 8.65081886340590e-01 1.07743222319750e-01 3.197438e+01 0.093 0.734 533
24 7.41935483870968e-01 8.64941995741777e-01 2.61053313440053e-01 2.643022e+01 0.137 0.500 280
25 7.74193548387097e-01 8.65433249788374e-01 4.14362165206138e-01 2.056916e+01 0.081 0.711 374
26 8.06451612903226e-01 8.67806367225160e-01 5.67653537891631e-01 1.471830e+01 0.071 0.643 559
27 8.38709677419355e-01 8.70841279609953e-01 7.20933592533481e-01 9.755915e+00 0.077 0.754 597
28 8.70967741935484e-01 8.70576649560447e-01 8.74235322866040e-01 5.873653e+00 0.105 0.703 744
29 9.03225806451613e-01 8.66137718710170e-01 1.02748030920223e+00 3.391863e+00 0.101 0.677 268
30 9.35483870967742e-01 8.63563899338629e-01 1.18076636418764e+00 1.937446e+00 0.066 0.828 586
31 9.67741935483871e-01 8.69235713509602e-01 1.33394269778577e+00 1.305873e+00 0.068 0.702 248
32 1.00000000000000e+00 8.81511000000000e-01 1.48675000000000e+00 1.025874e+00 0.060 0.731 239 The columns of the file correspond to the index of the point, the progress value, RC1, RC2, the free energy in kcal/mol, the standard error from bootstrap analysis, the RE, and the number of samples in the bin containing the point. Let's focus on the RE's.
[user@cluster] awk '{print $7}' path.9.RE.dat.wavg.9.dat
0.829
0.847
0.648
0.842
0.791
0.846
0.842
0.838
0.801
0.699
0.740
0.825
0.825
0.699
0.756
0.726
0.621
0.592
0.511
0.828
0.824
0.737
0.734
0.500
0.711
0.643
0.754
0.703
0.677
0.828
0.702
0.731[user@cluster] awk '{total += $7} END {print total/NR}' path.9.RE.dat.wavg.9.dat
0.739062The average RE is about 0.74, which indicates generally good phase space overlap. A good rule of thumb is that the RE should generally be above 0.6 to be considered a reliable estimate. If many points yield RE below 0.6 you will likely see a noisy PMF, indicating that either the machine learning model is poor, or you need additional sampling. The lower the RE, the more samples will be needed to make a reliable estimate. In this case, there are 3 points that yield RE less than 0.6, with the lowest being 0.5. These points occur on either side of the rate determining transition state, which are areas where the black and red profiles did not align as well. It makes sense that phase space overlap in these regions is imperfect and that gwTP makes the most significant correction here, thus reducing the RE.
In practice, one could run the simulations longer until the RE is no longer increasing. In the below figure, the PMF and resulting RE's from this tutorial (left) are compared the the results after performing gwTP with an additional 200 ps of production sampling on the final path (right).
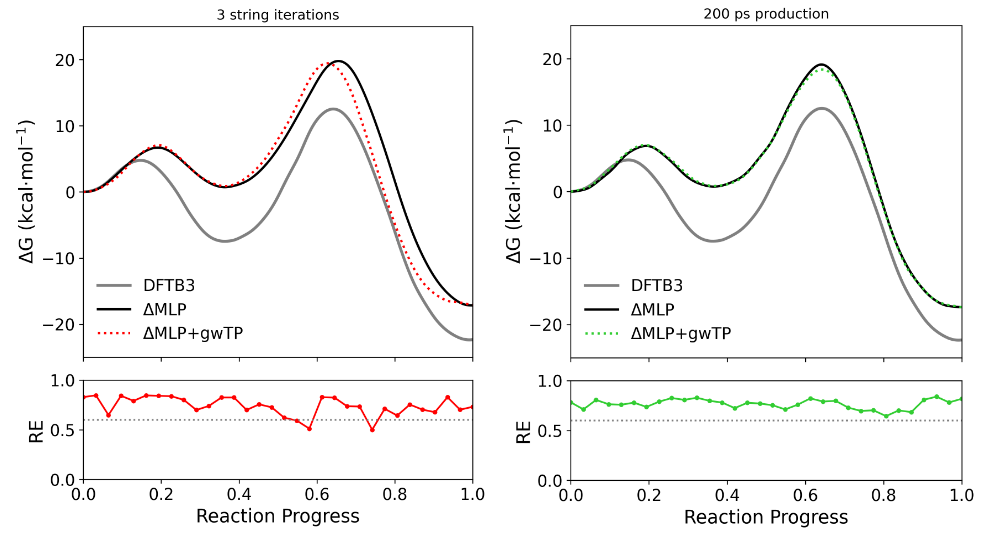
When exhaustive sampling is performed, all of the REs are above 0.6, and the machine learning and gwTP corrected curves match up nicely. It is difficult to validate a ΔMLP directly by comparing it to ab initio sampling because long-timescale sampling is intractable at the ab initio level. One may compare short time-scale sampling, but such PMFs will typically not represent equilibrium ensembles and may not be an accurate comparison. Therefore, gwTP is a valuable method of validation that avoids any costly ab initio dynamics while collecting equilibrium statistics. The ndfes-CheckEquil.py script in FE-ToolKit is a valuable tool to assess whether an umbrella sampling simulation has reached equilibrium.
In a previous session, you analyzed string simulations generated at the semi-empirical DFTB3 level. Here we will compare the difference in the PMF at the semi-empirical and your gwTP approximated ab initio level. You have been provided a file called DFTB3.dat in your gwTP directory. DFTB3.dat is the path file that we previously obtained when analyzing the DFTB3 strings that converged to the minimum free energy path. We will compare the machine learning and gwTP corrected PMFs with that of DFTB3 and PBE0.
[user@cluster] xmgrace -block path.9.opt.dat.wavg.9.dat -bxy 2:5 -block path.5.opt.dat.wavg.5.dat -bxy 2:5 -block DFTB3.dat -bxy 2:5 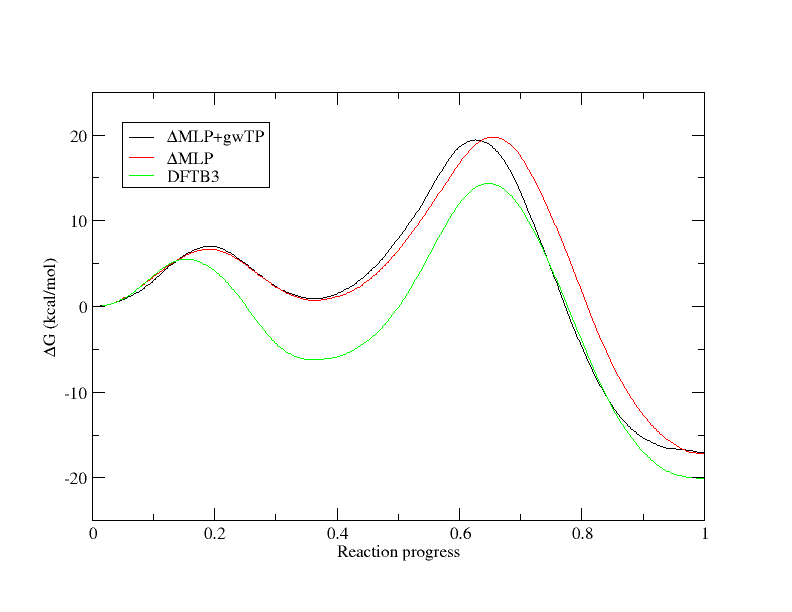
The PMFs have been aligned at y=0 for direct comparison. First let's focus on the ΔMLP+gwTP (black) and ΔMLP (red) curves. In general, both PMFs produce the same free energy trend with some discrepancies, and as we saw in the above figure, running the simulations for longer would have aided our estimate. Now let's focus on the DFTB3 (green) compared to the high level PMFs. Not only are the rate determining free energy barriers different, but the mechanistic interpretation is different when the higher level of theory is used. At the DFTB3 level (green) there is a stable intermediate state in which the proton transfer has occurred. This would suggest a proton would reside on the ligand a majority of the time. At the approximate PBE0 level, the intermediate is slightly higher in energy than the reactant state, suggesting the proton would likely be in rapid equilibrium between the cytosine residue and the ligand. This has implications for how one would interpret experimental observables such as pH dependence and highlights the importance of balancing the speed of the simulations with the accuracy of the Hamiltonian.