MM-to-QM/MM Free Energy "Bookend" Corrections using GFN2-xTB and QDπ2 machine learning potential.

Learning objectives

• Learn how to use sander.MPI to calculate MM-to-QM/MM free energy corrections using the reference potential method
• Learn to use edgembar to analyze the free energy from the sander output files
• Learn to apply a pre-trained DeePMD-kit machine learning correction potential

Relevant literature

• A recent article discussing the calculation of free energies using an indirect approach from a reference potential, Giese (2019).
• Some of the first works to develop the reference potential approach include Gao (1992) and Luzhkov (1992).
• Implementation of GFN2-xTB and DeePMD-kit into sander, Giese (2024).
• DeePMD-kit documentation

Introduction

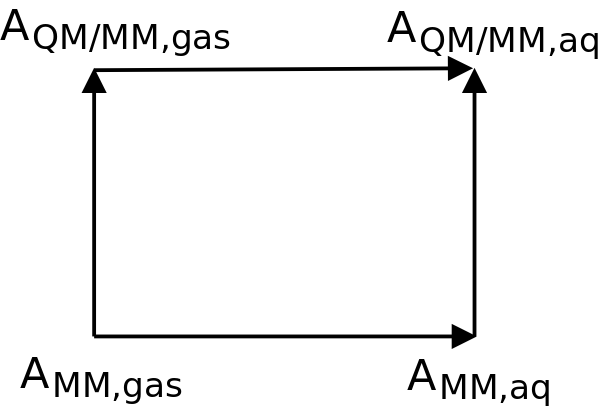
This tutorial will demonstrate how to calculate the absolute solvation free energy of a small molecule using a QM/MM potential energy function. Specifically, we shall estimate the solvation free energy of acetic acid using the GFN2-xTB semiempirical model supplemented with a QDπ2 machine learning potential. The method of calculation is based on the use of an indirect thermodynamic cycle, illustrated in Figure 1.

Figure 1. An indirect thermodynamic cycle for calculating the a QM/MM solvation free energy using a MM reference potential. The vertical arrows are the so-called "bookend" corrections. They are the free energy difference between the MM and QM/MM potential energy functions.

It is impractical to directly estimate the solvation free energy using a QM/MM potential [line 1 of Eq. \eqref{E:dAQMMM}] due to its high cost and the large amount of required sampling. \begin{equation}\label{E:dAQMMM} \begin{split} \Delta A_{\text{QM/MM},\text{solv}} =& A_{\text{QM/MM},\text{aq}} - A_{\text{QM/MM},\text{gas}} \\ =& \Delta A_{\text{MM},\text{solv}} + \Delta A_{\text{MM}\rightarrow\text{QM/MM},\text{aq}} - \Delta A_{\text{MM}\rightarrow\text{QM/MM},\text{gas}} \end{split} \end{equation} In contrast, a MM force field is sufficiently affordable to obtain reasonable estimates of ΔA_MM,solv [Eq. \eqref{E:dAMM}]. \begin{equation}\label{E:dAMM} \Delta A_{\text{MM},\text{solv}} = A_{\text{MM},\text{aq}} - A_{\text{MM},\text{gas}} \end{equation} Because the free energy is a state function, the sum of free energies along any closed path is zero. This is mathematically expressed by the second line in Eq. \eqref{E:dAQMMM}. In other words, the indirect thermodynamic approach calculates ΔA_QM/MM,solv from a MM reference potential by including "bookend corrections" [Eqs. \eqref{E:BEaq}-\eqref{E:BEgas}]. \begin{equation}\label{E:BEaq} \Delta A_{\text{MM}\rightarrow\text{QM/MM},\text{aq}} = A_{\text{QM/MM},\text{aq}} - A_{\text{MM},\text{aq}} \end{equation} \begin{equation}\label{E:BEgas} \Delta A_{\text{MM}\rightarrow\text{QM/MM},\text{gas}} = A_{\text{QM/MM},\text{gas}} - A_{\text{MM},\text{gas}} \end{equation} The bookend corrections often do not require extensive sampling because it does not involve a physical transformation of the system.

A bookend correction can be calculated from the thermodynamic integration (TI) [Eq. \eqref{E:TI}] or multistate Bennett acceptance ratio method (MBAR) by analyzing the equilibrium sampling produced by a λ-dependent potential energy function that transforms between MM and QM/MM potentials [Eq. \eqref{E:Ulam}]. \begin{equation}\label{E:TI} \Delta A_{\text{MM}\rightarrow\text{QM/MM}} = \int_{0}^{1} \left\langle \frac{\partial U}{\partial \lambda} \right\rangle_{\lambda} d\lambda \end{equation} \begin{equation}\label{E:Ulam} U(\mathbf{r};\lambda) = \lambda U_{\text{QM/MM}}(\mathbf{r}) + (1-\lambda) U_{\text{MM}}(\mathbf{r}) \end{equation} \begin{equation}\label{E:dUdlam} \frac{\partial U(\mathbf{r};\lambda)}{\partial\lambda} = U_{\text{QM/MM}}(\mathbf{r}) - U_{\text{MM}}(\mathbf{r}) \end{equation}

"Multisander" (i.e., the MPI parallel version of sander, sander.MPI) evaluates Eq. \eqref{E:Ulam} using a "groupfile" and a few key options in the &cntrl; namelist. The first line of the groupfile defines the MM potential energy (the λ=0 state), and the second defines the QM/MM potential energy (the λ=1 state). An example is shown in Figure 2.

The MM and QM/MM input files must be the exact same except for the activation/deactivation of the QM (and machine learning) potentials. The mdin file &cntrl; section must specify the following options:

• icfe=1 This causes the groupfile to be interpretted as defining a λ-dependent potential energy function.
• clambda=0.0 This is the value of λ (a floating point number between 0 and 1). The λ=0 state corresonds to the first line in the groupfile. Both the MM and QM/MM input files should specify the same clambda value.

The following is a list of options that may be different in the MM and QM/MM input files.

• ifqnt=0 The value of this option (appearing in the &cntrl; section) controls whether a QM/MM potential is applied.
• idprc=0 The value of this option (appearing in the optional &dprc; section) controls whether a DeePMD-kit machine learning correction is applied. The &dprc; section is only applicable if amber was configured with interface support to the DeePMD-kit library.
• qm_ewald=0 The value of this option (appearing in the &qmmm; section) controls whether periodic electrostatics are included in the QM calculation. One normally sets qm_ewald=0; however, when calculating a bookend calculation in the gas phase, one can turn off the periodic electrostatics.

Example MM and QM/MM inputs for the calculation of Eq. \eqref{E:BEaq} are shown in Figure 3.

Running the simulations

Because the potential energy is described using a groupfile, one needs the MPI version of sander and at least 2 CPU cores. On a slurm-based scheduling system, one can launch 2 (MPI) tasks on 1 node using 1 core per task with the following command, which one would write in their submission slurm script. The -ng 2 tells sander to expect to read 2 lines from the groupfile.

For accurate results, one should simulate several λ values, such as 0.0, 0.2, 0.4, 0.6, 0.8, and 1.0. The bookend transformations tend to require sampling of far fewer λ-states than alchemical transformations because the system is not undergoing a physical change. The free energy calculated from TI or MBAR requires equilibrium statistics; therefore, one should equilibrate each simulation before gathering production statistics.

Example

• Download example_mm2qmmm.inputs.tar.gz. The package includes files used to calculate Eqs. \eqref{E:BEaq} and \eqref{E:BEgas} for acetic acid in which a MM potential is transformed to GFN2-xTB QM/MM with QDπ2 machine learning corrections. The contents of the files are essentially those shown in Figures 2 and 3.
• You can unpack the files by typing: tar -xzf example_mm2qmmm.inputs.tar.gz. This will create a directory ./example_mm2qmmm/.
  • example_mm2qmmm/
    • RunExample.sh
    • MakeTemplateFiles.sh
    • MakeEquilAndProdDirs.sh
    • edgembar-bookend2dats.py
    • init/
      • mm.aq.*.rst7
      • mm.vac.*.rst7
    • common/
      • vac.parm7
      • aq.parm7
      • qdpi2.pb

  Figure 4. Description of the directory structure contained within example_mm2qmmm.inputs.tar.gz.
• Change directory to ./example_mm2qmmm/ and type bash RunExample.sh. The RunExample.sh script will prepare a series of groupfiles and corresponding MM and QM/MM input files. These files are organized into several subdirectories, named: prod01, prod02, prod03, prod04. These are 4 directories are used to perform independent trials that depart from structures extracted from MM simulations. The trial directories will contain 2 subdirectories: aq/ and vac which contain simulations for Eqs. \eqref{E:BEaq} and \eqref{E:BEgas}, respectively. The sampling within each environment is separated into two directories: equil/ and prod/, which are used to perform equilibration and production sampling, respectively.
  • example_mm2qmmm/
    • sub.sims.slurm
    • sub.ana.slurm
    • RunExample.sh
    • MakeTemplateFiles.sh
    • MakeEquilAndProdDirs.sh
    • edgembar-bookend2dats.py
    • init/
      • mm.aq.*.rst7
      • mm.vac.*.rst7
    • common/
      • vac.parm7
      • aq.parm7
      • qdpi2.pb
    • prod01/
prod02/
prod03/
prod04/
template/
      
      • aq/
vac/
        • equil/
prod/
          • mm2qmmm.*.groupfile
mm.*.mdin
qm.*.mdin

  Figure 5. Description of the directory structure after running the RunExample.sh script. The highlighted files and directories are created by the script. The prod01, prod02, prod03, prod04 are 4 independent trials starting from different snapshots extracted from previous MM simulations. These directories are copies of the template directory.
• The RunExample.sh script will prepare a sub.sims.slurm script. The submission script uses slurm arrays to perform the sampling in each trial directory. In other words, the 4 array values (#SBATCH --array=1-4) perform sampling in each of the 4 trial directories.
• After the simulations complete, the data can be extracted from the information stored in the files: prod*/*/prod/mm.*.mdout. For your convenience, you can download the necessary output files example_mm2qmmm.outputs.tar.gz. Unpacking the files with tar -xzf example_mm2qmmm.outputs.tar.gz will cause the files to be copied into the subfolder ./example_mm2qmmm. That is, unpack example_mm2qmmm.outputs.tar.gz in the same directory you unpacked example_mm2qmmm.inputs.tar.gz
  • example_mm2qmmm/
    • analysis/
      
    • prod01/
prod02/
prod03/
prod04/
      • aq/
vac/
        • equil/
prod/
          • mm.*.mdout

  Figure 6. Description of the directory structure contained within example_mm2qmmm.outputs.tar.gz.

Analysis

The MM and QM/MM mdout files contain the same potential energy and the ∂U/∂λ data; therefore, we will only look at the MM mdout files. To perform TI analysis, one must extract the ∂U/∂λ time series from the simulations of each λ-state in each environment (aq or vac) and trial (prod01, prod02, prod03, prod04). Similarly, MBAR analysis requires the potential energy of each state, U(r;λ'). Because this is a linear transformation, the potential energy of any intermediate state can be computed from the λ=0 and λ=1 states [Eq. \eqref{E:Ulam}]. Furthermore, the MBAR analysis only requires potential energy differences, so we will obtain the same free energy if -- for each frame, k -- we define the zero of energy to be U_MM(r_k). In which case, the potential energy of state λ' evaluated at frame k within the ensemble of state λ is given by Eq. \eqref{E:UMBAR}. \begin{equation}\label{E:UMBAR} \begin{split} U(\mathbf{r}_{\lambda k};\lambda^{\prime}) - U_{\text{MM}}(\mathbf{r}_{\lambda k}) = & \lambda^{\prime} \left[ U_{\text{QM/MM}}(\mathbf{r}_{\lambda k})-U_{\text{MM}}(\mathbf{r}_{\lambda k}) \right] \\ =& \lambda^{\prime} \frac{\partial U(\mathbf{r}_{\lambda k};\lambda)}{\partial \lambda} \end{split} \end{equation} The mdout files contain lines that look like:

 NSTEP =       50   TIME(PS) =    1020.100  TEMP(K) =   298.61  PRESS =     0.0
 Etot   =    -61089.2946  EKtot   =      5235.5357  EPtot      =    -66324.8304
 BOND   =         2.8694  ANGLE   =         4.6157  DIHED      =        17.6568
 1-4 NB =         0.4164  1-4 EEL =       -89.3041  VDWAALS    =      5313.5873
 EELEC  =    -42803.8431  EHBOND  =         0.0000  RESTRAINT  =         0.0000
 DV/DL  =   -143769.6429
 Ewald error estimate:   0.2471E-02
 ------------------------------------------------------------------------------

The example_mm2qmmm/sub.ana.slurm slurm submission file uses the example_mm2qmmm/edgembar-bookend2dats.py script to extract the relevant data from the mdout files and use edgembar to perform the analysis. The "bookend-to-dats" script takes a list of mdout filenames (e.g. prod01/aq/prod/mm.*.mdout) extracts the DV/DL data from each file, and writes the TI and MBAR timeseries in a format that can be analyzed using the edgembar program. The MakeAnalysis.sh script executes the script on the mdout files from each trial. The extracted outputs are written to a series of files: analysis/mm~qmmm/env/trial/dats/efep_tlam_elam.dat and analysis/mm~qmmm/env/trial/dats/dvdl_tlam.dat, where env is either aq or vac, trial is either t01, t02, t03, or t04, tlam is the lambda value used to simulate the trajectory, and elam is the lambda value corresponding to the energy within the file.

The sub.ana.slurm script then creates an XML input file to run edgembar. The XML file is provided as mm2qmmm/analysis/xml/mm~qmmm.xml, and it is shown in Figure 7.

<?xml version="1.0" ?>
<edge name="mm~qmmm">
	<env name="target">
		<stage name="STAGE">
			<trial name="t01">
				<dir>mm~qmmm/aq/t01/dats</dir>
				<ene>0.00000000</ene>
				<ene>0.20000000</ene>
				<ene>0.40000000</ene>
				<ene>0.60000000</ene>
				<ene>0.80000000</ene>
				<ene>1.00000000</ene>
			</trial>
			<trial name="t02">
				<dir>mm~qmmm/aq/t02/dats</dir>
				<ene>0.00000000</ene>
				<ene>0.20000000</ene>
				<ene>0.40000000</ene>
				<ene>0.60000000</ene>
				<ene>0.80000000</ene>
				<ene>1.00000000</ene>
			</trial>
			<trial name="t03">
				<dir>mm~qmmm/aq/t03/dats</dir>
				<ene>0.00000000</ene>
				<ene>0.20000000</ene>
				<ene>0.40000000</ene>
				<ene>0.60000000</ene>
				<ene>0.80000000</ene>
				<ene>1.00000000</ene>
			</trial>
			<trial name="t04">
				<dir>mm~qmmm/aq/t04/dats</dir>
				<ene>0.00000000</ene>
				<ene>0.20000000</ene>
				<ene>0.40000000</ene>
				<ene>0.60000000</ene>
				<ene>0.80000000</ene>
				<ene>1.00000000</ene>
			</trial>
		</stage>
	</env>
	<env name="reference">
		<stage name="STAGE">
			<trial name="t01">
				<dir>mm~qmmm/vac/t01/dats</dir>
				<ene>0.00000000</ene>
				<ene>0.20000000</ene>
				<ene>0.40000000</ene>
				<ene>0.60000000</ene>
				<ene>0.80000000</ene>
				<ene>1.00000000</ene>
			</trial>
			<trial name="t02">
				<dir>mm~qmmm/vac/t02/dats</dir>
				<ene>0.00000000</ene>
				<ene>0.20000000</ene>
				<ene>0.40000000</ene>
				<ene>0.60000000</ene>
				<ene>0.80000000</ene>
				<ene>1.00000000</ene>
			</trial>
			<trial name="t03">
				<dir>mm~qmmm/vac/t03/dats</dir>
				<ene>0.00000000</ene>
				<ene>0.20000000</ene>
				<ene>0.40000000</ene>
				<ene>0.60000000</ene>
				<ene>0.80000000</ene>
				<ene>1.00000000</ene>
			</trial>
			<trial name="t04">
				<dir>mm~qmmm/vac/t04/dats</dir>
				<ene>0.00000000</ene>
				<ene>0.20000000</ene>
				<ene>0.40000000</ene>
				<ene>0.60000000</ene>
				<ene>0.80000000</ene>
				<ene>1.00000000</ene>
			</trial>
		</stage>
	</env>
</edge>